Windoku
Windoku, NRC-Sudoku, Hypersudoku, Sudoku Hyper, or Four-square Sudoku is a Sudoku Variant with additional constraints. This format was first introduced in the Dutch newspaper NRC Handelsblad by Peter Ritmeester and the first playable online version by Chris McCusker.
Contents
Hidden Constraints
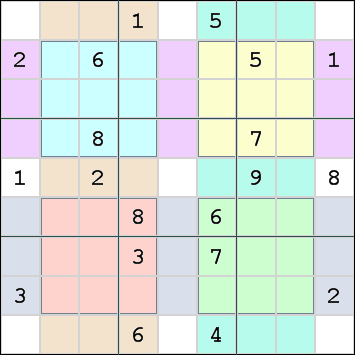
Although there are only 4 additional constraints (the 4 window panes) highlighted by the puzzle maker, the position of these 4 window panes indirectly creates 5 additional constraints. These are shown in the following picture.
- 1. Top-Left window pane
- the cyan 9 cells in rows 2, 3, 4 and columns 2, 3, 4
- 2. Top-Right window pane
- the yellow 9 cells in rows 2, 3, 4 and columns 6, 7, 8
- 3. Bottom-Left window pane
- the red 9 cells in rows 6, 7, 8 and columns 2, 3, 4
- 4. Bottom-Right window pane
- the green 9 cells in rows 6, 7, 8 and columns 6, 7, 8
- 5. Top Stiles
- The top-left window pane and the top-right window pane each require digits 1-9. This leaves the magenta cells for rows 2, 3 and 4 with the remaining set of 1-9.
- 6. Bottom Stiles
- The bottom-left window pane and the bottom-right window pane each require digits 1-9. This leaves the grey cells for rows 6, 7 and 8 with the remaining set of 1-9.
- 7. Left Rails
- The Top-left window pane and the bottom-left window pane each require digits 1-9. This leaves the light brown cells for columns 2, 3 and 4 with the remaining set of 1-9.
- 8. Right Rails
- The Top-right window pane and the bottom-right window pane each require digits 1-9. This leaves the dark cyan cells for columns 6, 7 and 8 with the remaining set of 1-9.
- 9. Corners
- All the cells in the grid belong to non-overlapping groups, except the white cells. This is the last group which requires digits 1-9.
Solving Techniques
The solving techniques for a Windoku are similar to those of regular Sudoku. The extra constraints are placed in such a way that there are many more intersections to deal with. Each additional constraint can contain subsets and strong links which could be used in coloring techniques.
There are fewer Unique Rectangles in the grid, because not all 468 possible unique rectangles for a standard Sudoku are located in exactly 2 additional houses.
Minimum Number of Givens
Valid Windokus with 11 givens exist. However, it is not known whether this is the minimum number of givens. See this page for examples for such Windokus.