XY-Chain
A XY-Chain is a chain of cells which each contain only 2 candidates.
Because the chain is entirely made up by bivalue cells, the link between the 2 candidates in each cell cause strong inference, which allows us to use weak inference between the cells.
The shortest XY-Chain is an XY-Wing with only 3 cells.
A XY-Chain is both a Double Implication Chain and a Alternating Inference Chain.
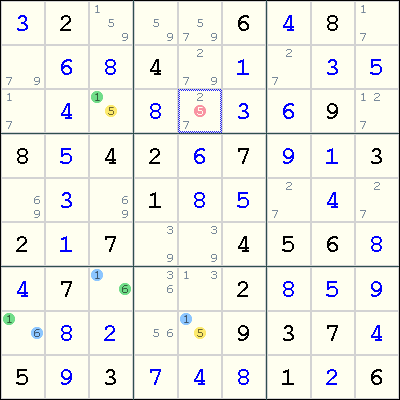
Example
The following example shows a XY-chain resulting in an elimination.
This chain involves four cells. In Eureka notation:
(5=1)r3c3-(1=6)r7c3-(6=1)r8c1-(1=5)r8c5
What does this XY-chain mean? Note that both ends of the chain involves the digit 5 as a candidate. Now, if r3c3<>5, then we have r3c3=1, which implies r7c3=6 and r8c1=1, so r8c5=5. Similarly, by reversing the direction, if r8c5<>5, then r3c3=5. Thus, this is a Double Implication Chain and we showed that either r3c3=5 or r8c5=5. This means that any cell that is seen by both r3c3 and r8c5 cannot contain the digit 5, so we eliminate 5 from r3c5.
A single inference xy-chain is also useful for finding a wrap rather than a trap as in the above example. To illustrate this consider rows 6 and 7 of a puzzle shown below.
| Row 6 | | | 4 | 1 | 278 | | | 23 | 37 | 6 | | | 9 | 78 | 5 | | |
| Row 7 | | | 9 | 37 | 1347 | | | 5 | 34 | 148 | | | 6 | 78 | 2 | | |
The 3 digits in column 5 are a conjugate pair. Now r7c5 = 3 implies r7c2 = 7 implies r7c8 = 8 implies r6c8 = 7 implies r6c5 = 3, which is a wrap. Therfore r7c5 = 4 and r6c5 = 3.