Alternating Inference Chain
Contents
Definition
An Alternating Inference Chain, better known by its acronym AIC, is a chain of premises, linked by alternating strong and weak inferences.
The vertices in the chain are premises: statements or assertions that may be either true or false. The simplest premise concerns the candidate values of individual cells:
- r1c1 has the value 3
- r5c6 cannot have the value 4
However, a premise may involve groups of cells or complex patterns such as Almost Locked Sets:
- one of the cells r2c2, r2c3, or r2c4 has the value 5
- the almost locked set consisting of cells r4c4, r4c5, and r5c4 cannot have the value 3
The inferences that form the links between the premises in the chain are either strong or weak.
A strong inference asserts that the two premises cannot both be false. For example, if cell r3c5 has only two candidate values 3 and 4, these two premises can be strongly linked:
- r3c5 has the value 3
- r3c5 has the value 4
A weak inference asserts that both premises cannot be true. For example:
- r3c5 has the value 3
- r3c4 has the value 3
Note that the two premises in the preceding strong link example also can be weakly linked, since they can't both possibly be true at the same time.
Conventional notation uses double lines (=) to indicate strong inferences and single lines (-) to indicate weak inferences.
It is possible to write AICs with the Eureka notation system.
Non-looping AICs
An AIC chains together premises using alternating strong and weak inferences. The simplest AICs look like this (A, B, C, and D represent the premises):
- A=B-C=D
- A-B=C-D
The power of an AIC is that the end points of such a chain are always linked.
Proof: The first AIC shown above can be written as the Boolean algebraic expression: (A|B)&(~B|~C)&(C|D) For this expression to be true, the truth table looks like this: A B C D ---------- F T F T T F F T T F T F T F T T T T F T Note that in no case is it possible for both A and D to be false. A and D are thus strongly linked. Similarly, we can write the second AIC shown above as: (~A|~B)&(B|C)&(~C|~D) For this expression to be true, the truth table looks like this: A B C D ---------- F F T F F T F F F T F T F T T F T F T F Note that in no case is it possible for both A and D to be true. A and D are thus weakly linked.
The goal here is to use the link (inference) between the endpoints of the AIC to perform candidate eliminations. For example, suppose that an AIC has these two premises as endpoints, linked strongly:
- r3c3 has the value 3
- r6c6 has the value 3
The strong link means that 3 must be in one or the other (or maybe both) of the two cells. 3 can be eliminated as a candidate value from r3c6, which sees both of the cells involved in the AIC's endpoint premises.
An interesting case occurs where there is mutual visibility between cells involved in the AIC's endpoint premises. For example, an AIC with the strongly linked endpoint premises:
- r4c2 has the value 4
- r5c2 has the value 5
The strong link between these premises (both cannot be false) means that we can eliminate 4 as a candidate value from r5c2 and 5 as a candidate value from r4c2.
AIC Loops
An AIC can form a loop if the chain's endpoint premise can be linked to the starting premise:
A=B-C=D-E=F-A
When the AIC forms a loop, the loop can be broken at any of the links and any eliminations from the resulting chain can be performed. Thus, the loop shown in the example above yields these chains:
- A=B-C=D-E=F
- B-C=D-E=F-A
- C=D-E=F-A=B
- D-E=F-A=B-C
- E=F-A=B-C=D
- F-A=B-C=D-E
A Further Example
This example shows the Eureka notation for an AIC.
(1)r1c1=(1)r1c5-(1)r5c5=(1)r6c6 => r6c1<>1 This chain has four premises:
- r1c1 has the value 1
- r1c5 has the value 1
- r5c5 has the value 1
- r6c6 has the value 1
The chain links represent the following inferences:
- At least one of r1c1 or r1c5 must be 1 (strong inference)
- r1c5 and r5c5 cannot both be 1 (weak inference)
- At least one of r5c5 or r6c6 must be 1 (strong inference)
The chain proves that either r1c1 or r6c6 must contain digit 1. Therefore r6c1 cannot contain digit 1.
When the premises of an AIC involve only individual candidate values, then it is either a X-Chain, a XY-Chain or some combination of X-Chains and XY-Chains.
An Example Involving Groups in Premises
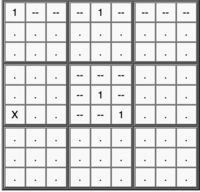
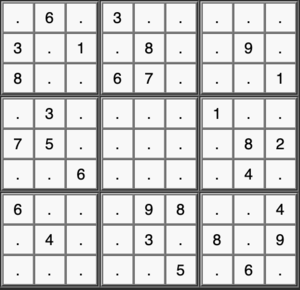
Consider this Sudoku puzzle:
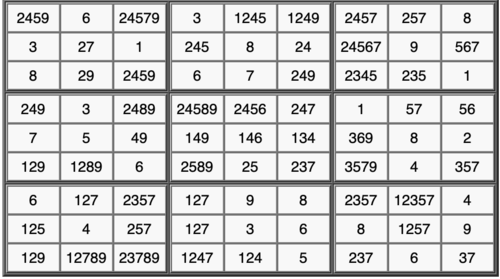
After simple eliminations, we arrive at this candidate grid:
This AIC can be formed (shown in condensed Eureka notation):
(1)r1c6=r5c6=(3-7)r6c6=grp(7)r6c79-r4c8-(5=6)r4c9-r2c9=(6-4)r2c7=grp(4)r2c46 => r1c6<>4
Expanded, the premises and linking inferences are:
- r1c6 is 1 or r5c6 is 1 (strong inference)
- r5c6 cannot be both 1 and 3 (weak inference)
- r5c6 or r6c6 is 3 (strong inference)
- r6c6 cannot both be 3 and 7 (weak inference)
- r6c6 is 7 or one of the cells in the group {r6c7, r6c9} is 7 (strong inference)
- neither of the cells in the group {r6c7, r6c9} can be 7 if r4c8 is 7, and vice versa (weak inference)
- r4c8 must be either 7 or 5 (strong inference)
- r4c8 and r4c9 cannot both be 5 (weak inference)
- r4c9 must be either 5 or 6 (strong inference)
- r4c9 and r2c9 cannot both be 6 (weak inference)
- one of r2c9 or r2c7 is 6 (strong inference)
- r2c7 cannot be both 6 and 4 (weak inference)
- r2c7 is 4 or one of the cells in the group {r2c4, r2c6} is 4 (strong inference)
r1c6 (start of the AIC) and all of the cells in the group {r2c4, r2c6} (end of the AIC) are mutually visible. Thus, r1c6 cannot be 4 and neither of {r2c4, r2c6} can be 1. We can thus eliminate 4 as a candidate from r1c6.