Difference between revisions of "Crossover"
(Created page with "'''Crossover''' is a basic technique for Sudoku-X, which says that if there are exactly two cells '''A''' and '''B''' with candidate '''X''' along a diagonal...") |
|||
| Line 9: | Line 9: | ||
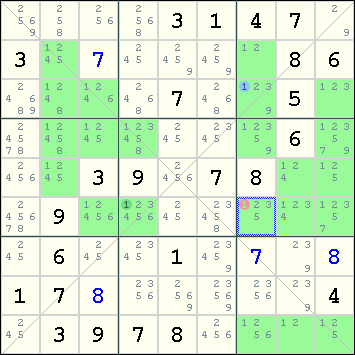
One of the diagonals has exactly two cells having '''1''' as a candidate: '''r3c7''' and '''r6c4'''. Both of these cells see '''r6c7'''. Hence, '''1''' can be eliminated from '''r6c7'''. | One of the diagonals has exactly two cells having '''1''' as a candidate: '''r3c7''' and '''r6c4'''. Both of these cells see '''r6c7'''. Hence, '''1''' can be eliminated from '''r6c7'''. | ||
| − | |||
| − | |||
| − | |||
== See Also == | == See Also == | ||
Latest revision as of 02:55, 20 January 2022
Crossover is a basic technique for Sudoku-X, which says that if there are exactly two cells A and B with candidate X along a diagonal, then X can be eliminated from the other two cells that are seen by both A and B. Crossover can also be applied when there are exactly three cells with the candidate X along the diagonal, as long as one of the cells is r5c5, and the other two cells A and B are located at the same distance away from r5c5.
In other words, the crossover rule is simply Common Peer Elimination applied to the diagonals of the Sudoku-X. When there are exactly two cells along the diagonal having the candidate X, SudoCue replicates crossover using Simple Colors, i.e., a X-Chain containing two cells.
Example
The following example illustrates the crossover technique.
One of the diagonals has exactly two cells having 1 as a candidate: r3c7 and r6c4. Both of these cells see r6c7. Hence, 1 can be eliminated from r6c7.