Difference between revisions of "Hypersudoku"
(Created page with "==Hypersudoku== '''Hypersudoku''', '''Windoku''', '''NRC-Sudoku''', or '''Four-square Sudoku''' is one of the Sudoku Variations with additional constraints. This f...") |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 61: | Line 61: | ||
<tr> | <tr> | ||
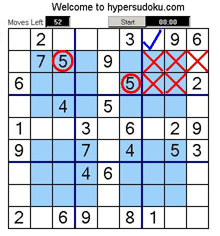
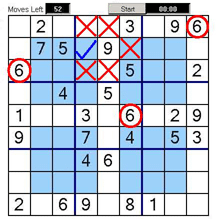
<td width="50%" border="0"><h3>Example 7</h3>If we look at the top right blue square, it has to have a nine in it. The top corner square (in red) that overlaps the blue square already has a nine in it (circled in red). The middle top square that also overlaps the blue square has a nine already in it (circled in red). The middle right-hand square also has a nine in it which only leaves the square with the blue tick as the only possible square for nine to go in in the top right blue square.<br /><br />As you can see the logic of the overlapping squares is quite helpful for solving these puzzles. </td> | <td width="50%" border="0"><h3>Example 7</h3>If we look at the top right blue square, it has to have a nine in it. The top corner square (in red) that overlaps the blue square already has a nine in it (circled in red). The middle top square that also overlaps the blue square has a nine already in it (circled in red). The middle right-hand square also has a nine in it which only leaves the square with the blue tick as the only possible square for nine to go in in the top right blue square.<br /><br />As you can see the logic of the overlapping squares is quite helpful for solving these puzzles. </td> | ||
| − | <td width="50%" border="0"> [[Image:Move7. | + | <td width="50%" border="0"> [[Image:Move7.jpg]]Figure |
8<br /></td> | 8<br /></td> | ||
| Line 69: | Line 69: | ||
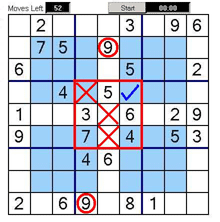
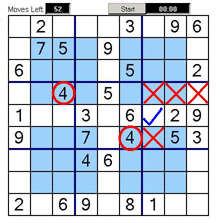
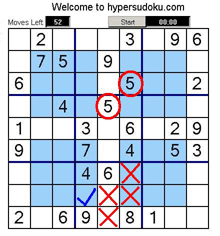
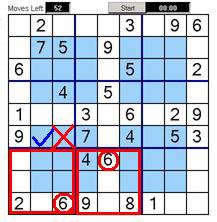
<h3>Example 8</h3>In this example if we look at the bottom left blue square, it has to have a six in it. The bottom corner square (in red) that overlaps the blue square already has a six in it (circled in red). This six is also the only six that can exist in this column so that eliminates the top middle blue square (marked with red cross) .The middle bottom square that also overlaps the blue square has a six already in it (circled in red). This only leaves the square with the blue tick as the only possible square for six to go in in the bottom right blue square.<br /><br />As you can see the logic of the overlapping squares is quite helpful for solving these puzzles. </td> | <h3>Example 8</h3>In this example if we look at the bottom left blue square, it has to have a six in it. The bottom corner square (in red) that overlaps the blue square already has a six in it (circled in red). This six is also the only six that can exist in this column so that eliminates the top middle blue square (marked with red cross) .The middle bottom square that also overlaps the blue square has a six already in it (circled in red). This only leaves the square with the blue tick as the only possible square for six to go in in the bottom right blue square.<br /><br />As you can see the logic of the overlapping squares is quite helpful for solving these puzzles. </td> | ||
| − | <td width="50%" border="0"> [[Image:Move8. | + | <td width="50%" border="0"> [[Image:Move8.jpg]]Figure |
| − | + | 9<br /></td> | |
</tr> | </tr> | ||
</table> | </table> | ||
Latest revision as of 19:52, 22 July 2025
Contents
Hypersudoku
Hypersudoku, Windoku, NRC-Sudoku, or Four-square Sudoku is one of the Sudoku Variations with additional constraints. This format was first introduced in the Dutch newspaper NRC Handelsblad by Peter Ritmeester and the first playable online version by Chris McCusker.
How to Play Hypersudoku
This game requires no mathematics skills. It is purely a logic game with the only prerequisite to be able to count to nine.
Hypersudoku Rules
The rules for playing hypersudoku are very simple.
1. All rows must have all the numbers from 1 - 9 in them (none can be repeated). There are 9 rows in the game.
2. All columns must have all the numbers from 1 - 9 in them (none can be repeated). There are 9 columns in the game.
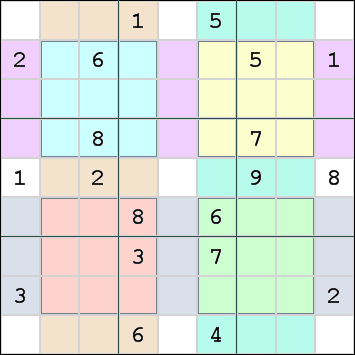
3. All 3x3 squares must have all the numbers from 1 - 9 in them (none can be repeated). There are 13 squares in the game. There are the 9 underlaying 3x3 squares (divided by the dark blue lines) and the 4 overlaying (shown in light blue in the following diagrams).
Hypersudoku Logic
Hidden Constraints
Although there are only 4 additional constraints mentioned by the publisher, the position of these 4 windows indirectly creates 5 additional constraints. These are shown in the following picture.
Solving Techniques
The solving techniques for a Windoku are similar to those of regular Sudoku. The extra constraints are placed in such a way that there are many more intersections to deal with. Each additional constraint can contain subsets and strong links which could be used in coloring techniques.
There are fewer Unique Rectangles in the grid, because not all 468 possible unique rectangles for a standard Sudoku are located in exactly 2 additional houses.
Minimum Number of Givens
Valid Windokus with 11 givens exist. However, it is not known whether this is the minimum number of givens. See this page for examples for such Windokus.