Multiple Crossover
In Sudoku Variants with additional diagonals like Sudoku-X and Argyle Sudoku, there are some techniques that are very similar to Crossover and Double Crossover.
Contents
Triple Crossover
Example 1
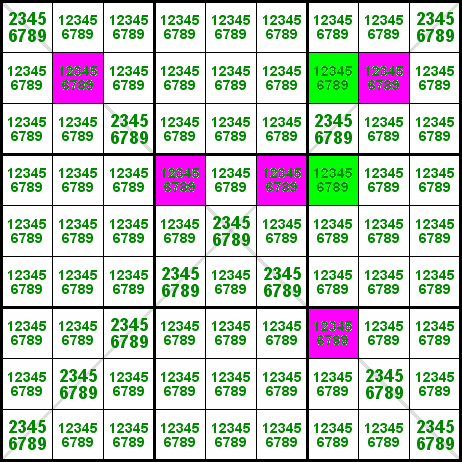
The pink cells are the only cells with the candidate 1 in the 2 diagonals of this Sudoku-X. Because the candidate 1 is not present in the common cell r5c5, the pink cells must contain exactly 2 occurrences of the digit 1. Due to the fact that the green cell at r2c7 sees (i.e., is weakly linked to) the cells r2c2, r2c8 and r7c7, a 1 at this position would constrain the 2 occurrences of the digit 1 in the diagonals to r4c46, which is impossible, since they are peers of each other.
Similarly, a 1 in the green cell at r4c7 would constrain the 2 occurrences of the digit 1 in the diagonals to r2c28, which is again impossible.
Therefore, with respect to the triple crossover we can safely eliminate the candidate 1 from the green cells.
Note: This scenario is referred to as a triple crossover because each of the green cells sees 3 pink cells.
Example 2
There is also another variant of this technique:
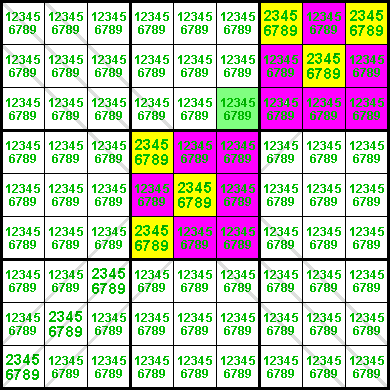
The logic here is analogous to that described in the first example. The pink cells represent the possible candidate positions for digit 1 in row 6 and row 8. Since these two groups are disjoint (i.e., do not overlap), they must contain 2 occurrences of the digit 1. If r3c7 or r5c5 would contain a 1, this would force the two 1s in these two rows into r68c5 and r68c7, respectively.
Therefore, with respect to the triple crossover we can safely eliminate the candidate 1 from the green cells.
Quadruple Crossover
Example 1
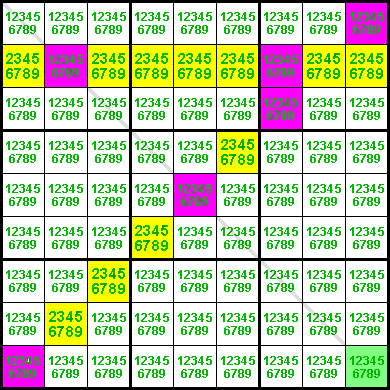
A similar logic still works here, where the green cell sees 4 pink cells (hence the term "quadruple crossover"):
Example 2
Or in its diagonal variant:
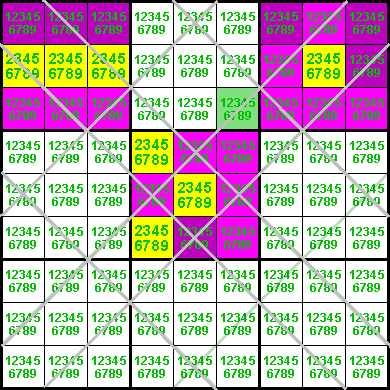
The 2 houses marked in yellow (row 2 and D/), taken together, must contain 2 occurrences of the digit 1, since a 1 cannot exist within the overlapping region (r2c8). If the green cell at r9c9 were to contain a 1, it would constrain both occurrences to r23c7, which is impossible, since they both belong to the same column. We can therefore safely eliminate the 1 from r9c9.
n-tuple Crossover
Example 1
If we have more diagonals we get more complicated crossovers. Here a 10-tuple crossover in a sudoku with the bold X pattern (6 diagonals).
Example 2
And a 13tuple crossover in an Argyle Sudoku:
In this more complicated example, the three boxes with the yellow background are disjoint, and must therefore contain 3 occurrences of the digit 1, which are locked in the cells marked in light and dark pink. The green cell sees all light pink cells. Therefore, if the green cell were to contain a 1, it would constrain the three 1s in boxes 1, 3 and 5 to the cells marked in dark pink. However, this is impossible, because the dark pink cells can only accommodate 2 of these 3 occurrences in total, due to the fact that r2c9 and r6c5 see each other.
General Rule
From the above examples, we can formulate the general principle as follows:
"If all cells with a certain candidate in N pairwise disjoint, locked, groups (N > 1) that are not weakly linked to a certain green cell are located in (N - 1) pairwise disjoint groups and the green cell isn't in these N groups, then the green cell cannot have this candidate."
Note: To be disjoint is not really necessary. The technique is still valid if all common cells belonging to a pair of groups either do not have the candidate (as is the case in some of the examples above), or are weakly linked to the green cell. In the latter case, if one of the common cells were to contain the digit in question, the fact that it sees the green cell would directly prevent a 1 from existing in the green cell, even though the logic described above would break down.