Aligned Pair Exclusion
Aligned Pair Exclusion or APE is a solving technique in which the solver checks combinations of digits in a pair of cells located in an intersection.
It is a very laborious technique, which may explain why it is not so popular. Many APE moves can also be replicated by the easier XY-Wing and XYZ-Wing techniques. Some APE moves can also be replicated by the ALS-XZ rule.
Contents
Examples
Below are two examples that illustrate the APE move.
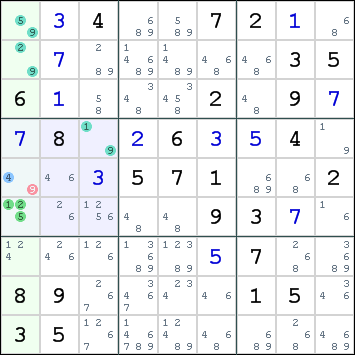
Example 1
|
We are examining the pair r5c1 and r6c1. Their respective candidates are: 4,9 1,2,5 The following configurations are possible: 4+1 9+1* 4+2 9+2* 4+5 9+5* The combination 1+9 is already present in r4c3, which can see both cells. This combination would eliminate all candidates from this cell, so it must be invalid. The same reasoning can be used for the combination 2+9 and r2c1, and also for 5+9 and r1c1. Effectively, all combinations which include a 9 in r5c1 are invalid. As a result, we can eliminate this candidate. The remaining candidate 4 can be placed in r5c1. |
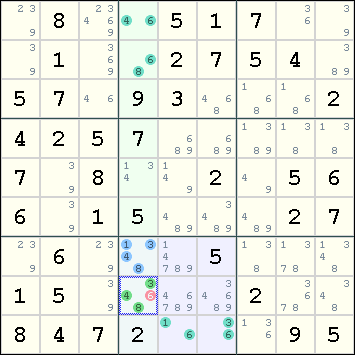
Example 2
|
Here we enumerate all the combinations of the cells r7c4 and r8c4. Their respective candidates are: 1,3,4,8 3,4,6,8 The enumeration goes as follows: 1+3 1+4 1+6* 1+8 3+4 3+6* 3+8 4+3 4+6* 4+8 8+3 8+4 8+6* Due to the cells r1c4, r2c4, r9c5, r9c6, four of the combinations are not permissible. When we strike off these illegal combinations, we find that all combinations with 6 are removed. Hence we can remove 6 from r8c4. |
Extensions
Aligned Pair Exclusion can be extended to Aligned Triple Exclusion and so on. In fact, the set of cells to be enumerated does not need to be aligned at all. See Subset Exclusion.
Yet another extension for Aligned Pair Exclusion is to consider not just bivalue cells, but also pairs of cells having a total of three candidates X, Y and Z. Then we can exclude the X+Y, X+Z and Y+Z combinations. See Andrew Stuart's Advanced Strategies (under Aligned Pair Exclusion - Type 2) for two examples.
Relation between APE and ALS-XZ
Consider the APE without any extensions. To apply the APE, we are looking at the intersection of two constraints, one a line and the other a box. Suppose we enumerate the combination of two cells A and B within the intersection, leading to the elimination of some candidate in A. If one of the two constraints has only one cell X involved in the application of APE, then we can replicate this APE with an ALS-XZ rule which leads to the same elimination, where the two ALSs are: (a) the cell X itself, and (b) the cell B plus the cells in the other constraint that participates in the APE.
Hence, Example 1 above can be recast as an ALS-XZ, with the first ALS being r4c3 and the second ALS being r126c1, the restricted common being 1, eliminating all instances of digit 9 that is seen by all cells in both ALSs that has 9 as a candidate. This eliminates 9 from both r2c3 and r5c1.