ALS-XZ
The ALS-XZ rule is a solving technique that uses two Almost Locked Sets. It is the easiest of the ALS techniques, but still a technique that is rarely used by the average Sudoku player.
Make sure you understand the concept of Almost Locked Sets before you proceed.
How it works
The ALS-XZ rule says that if A and B are Almost Locked Sets (or ALSes), and X is restricted common to A and B, then no other common candidate (let's call it Z) can appear outside of A and B in a cell that can see all the Z candidates in both A and B.
Note that it doesn't matter whether or not Z is also restricted common to A and B, except that if Z is also restricted common, we can remove X as a candidate of any cells outside A and B that can see all the X candidates in both A and B. That is, each candidate, in turn, gets to play the role of restricted common, giving us the chance to eliminate the other candidate from outside cells.
This technique is best explained using an example:
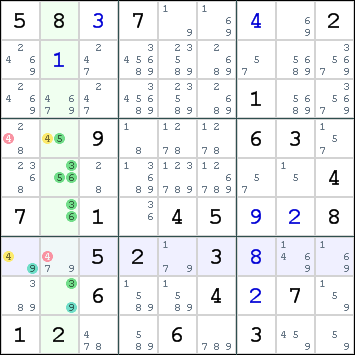
There are two Almost Locked Sets:
- r4568c2 (4 cells) with digits 3,4,5,6,9
- r7c1 (1 cell) with digits 4,9
Digit 9 is restricted common to both sets. We call this the X digit. All candidates for digit 9 in both sets can see all candidates in the other set. In fact, there is only one candidate for digit 9 in each set, both are located in box 7. This box can have only a single digit 9, so one of the sets will not contain digit 9.
Digit 4 is also present in both sets. This is the Z digit. Because we know that digit 9 will not be present in one of these two sets, that set will be locked for the remaining digits and must therefore contain digit 4.
All cells that can see all candidates for digit 4 in both sets cannot contain this digit. Hence, we can eliminate digit 4 from r4c1 and r7c2.
String for original puzzle:
580700002000000000000000100009000630000000004701045008005203000006004070120060300
ALS notation
Advanced players are like doctors. They like compact incomprehensible writing. In a solving path, you might encounter this ALS-XZ move in the following format:
A=r4568c2, B=r7c1, X=9, Z=4 => r4c1,r7c2<>4
A is the first ALS, B is the second ALS, X is the restricted common digit and Z is the common digit that causes the eliminations.
As an alternative, an ALS move can be presented as a chain. The ALS-XZ move can be written like this in Eureka notation:
(4)r4c1|r7c2-(4=9)r7c1-(9=3564)r4568c2-(4)r4c1|r7c2 => r4c1|r7c2<>4