Sashimi Swordfish
A Sashimi Swordfish is a Finned Swordfish that has no candidate for the underlying Swordfish in the box containing the fin.
This is only one member of the large family of fish patterns. The Sashimi Swordfish uses 3 rows, 3 columns and a box. Other sizes of Sashimi Fish are Sashimi X-Wing and Sashimi Jellyfish.
Contents
Sashimi Swordfish in the Rows
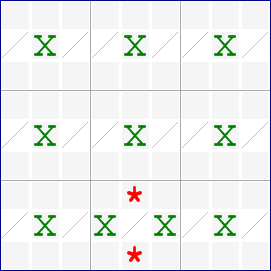
- Consider the candidates for a single digit. When all candidates in 3 rows are located in 3 columns and a box which contains at least one of these columns, you may remove all candidates from this box which are located on one of the 3 columns. A Sashimi Swordfish does not have any candidates in the extra box which are located on the intersection of a defining row and a covered column.
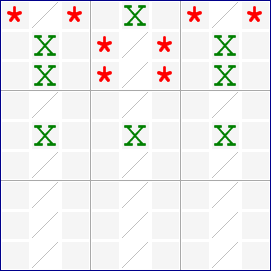
Either one of the X candidates in box 8 can be present. If there were a candidate in r8c5, this would be a Finned Swordfish.
Example
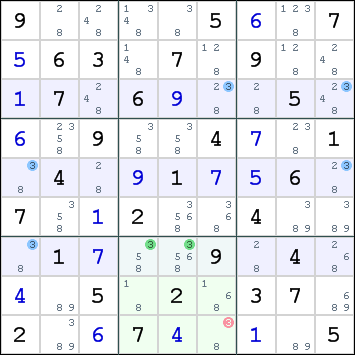
Sashimi Swordfish for digit 3 in rows 3,5,7 and columns 1,6,9 with a fin in box 8.
Sashimi Swordfish in the Columns
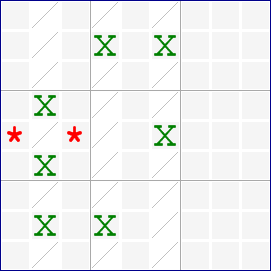
- Consider the candidates for a single digit. When all candidates in 3 columns are located in 3 rows and a box which contains at least one of these rows, you may remove all candidates from this box which are located on one of the 3 rows. A Sashimi Swordfish does not have any candidates in the extra box which are located on the intersection of a defining column and a covered row.
This diagram shows that each defining column can have 2 or 3 candidates, and the defining columns that intersect the extra box can have only a single candidate that belongs to the underlying Swordfish.
Example
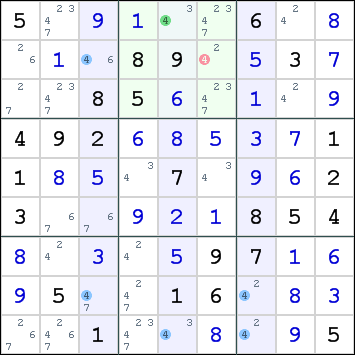
Sashimi Swordfish for digit 4 in columns 3,5,7 and rows 2,8,9 with the fin in box 2.
Cascading Locked Candidates
When there are 2 secondary lines present in the box with the fin, upto 4 candidates can be eliminated. As a result, all remaining candidates in this box will be located on a single row or column (row 1 in the diagram). This triggers a Locked Candidates move that causes additional eliminations on this line.