Locked Candidates
A solving technique that uses the intersections between lines and boxes.
Aliases include: Intersection Removal, Line-Box Interaction. The terms Pointing and Claiming/Box-Line Reduction are often used to distinguish the 2 types.
This is a basic solving technique. When all candidates for a digit in a house are located inside the intersection with another house, we can eliminate the remaining candidates from the second house outside the intersection.
Contents
Type 1 (Pointing)
All the candidates for digit X in a box are confined to a single line (row or column). The surplus candidates are eliminated from the part of the line that does not intersect with this box.
.-------.-------.-------.
| * * * | * * * | X X X |
| | | - - - |
| | | - - - |
'-------'-------'-------'
Legend:
X : cell which may contain a candidate for digit X
- : cell which does not contain a candidate for digit X
* : cell from which we may eliminate the candidates for digit X
Depending on the number of available candidates in the intersection, this technique is also known as a Pointing Pair or Pointing Triple.
Type 2 (Claiming or Box-Line Reduction)
All the candidates for digit X in a line are confined to a single box. The surplus candidates are eliminated from the part of the box that does not intersect with this line.
.-------.-------.-------. | - - - | - - - | X X X | | | | * * * | | | | * * * | '-------'-------'-------'
Example
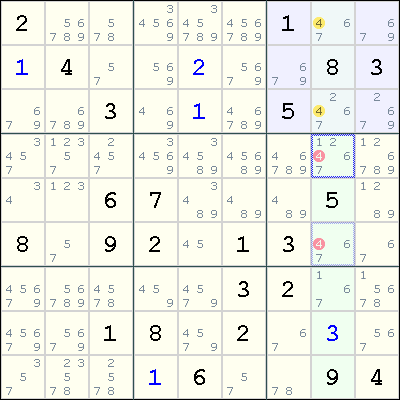
There is a Locked Candidates Type 1 (Pointing) for the digit 4 as shown in yellow. The red candidates can be eliminated.
Killer Sudoku
The cages in Killer Sudoku can offer more modes of the locked candidates technique. We use two examples to illustrate such techniques, both taken from Ruud's Assassin 1.
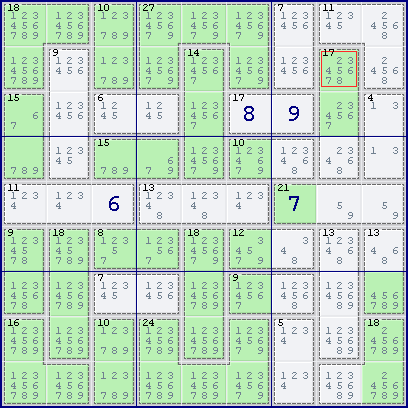
For the first example shown below, consider the 17[3] cage in column 8.
The possible cage combinations of the 17[3] cage in column 8 are {2,7,8} or {3,6,8} or {4,5,8} or {4,6,7}. However, in column 8, all cells that has 7 as a candidate are the cells in the 17[3] cage. Therefore, we can strike off the combinations {3,6,8} and {4,5,8}, leaving the combinations {2,7,8} or {4,6,7}. This implies that we can eliminate 3 and 5 from all cells in the cage.
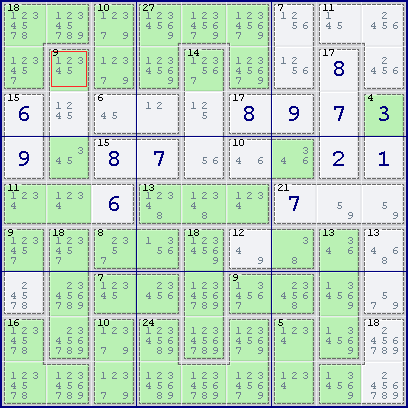
For the second example shown below, consider the 9[3] cage in column 2.
The possible cage combinations of the 9[3] cage in column 2 are {1,3,5} or {2,3,4}. Since both combinations contain the digit 3, this means that one of the cells in the 9[3] cage must contain the digit 3. Hence, 3 can be eliminated from all other cells in column 2.