Forcing Net
A Forcing Net shows a contradiction or a verity which is caused by testing a candidate. Also known as Generalized Forcing Chain. The term Contradiction Net is also used when the Forcing Net is used to derive a contradiction.
There are several techniques similar to Forcing Nets, like Trial & Error, Tabling and Bowman Bingo. Unlike a Forcing Chain, which requires a single stream of implications, a Forcing Net allows branching and merging, making it a lot more complicated than a single chain. Whenever possible, players avoid this solving technique.
How it works
The player selects a candidate to be tested. When this candidate belongs to a bivalue cell, finding a contradiction allows the player to place the remaining candidate in that cell. The tested candidate is assumed to be true and the implications are analyzed until a contradiction is found or no further progress can be made.
Here is an example:
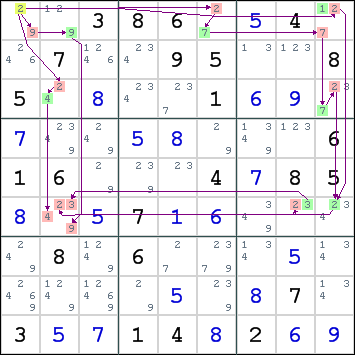
This is the Forcing Net shown in the picture:
| r1c1<>9 => r1c2=9 => r6c2<>9
r1c1=2 =>| r3c2<>2 => r3c2=4 => r6c2<>4
| r1c6=7 => r1c9<>7 => r3c9=7 => r3c9<>2 =>|
| r1c9<>2 => | r6c9=2 =>| r6c8=3 => r6c2<>3
| r6c2<>2
The initial placement causes 4 branches, 2 of them merging further down the net and branching off again. Together, they eliminate all 4 candidates in r6c2, which leaves this cell without any candidates.
As a result, we can eliminate candidate 2 from r1c1.
Note
There is a disagreement over using Contradiction Nets to solve Sudokus puzzles. While some players make extensive use of Contradiction Nets since it is entirely logical from an angle, other players have accused that using Contradiction Nets is not anything different from using Ariadne's Thread.