Braid Analysis
Braid Analysis or Braiding is a solving technique that analyzes the way digits are placed in a chute. The basis for this technique is the discovery of traveling pairs. These are formed because there is only a limited number of ways 3 digits can "travel" through a chute.
Contents
Braids and Ropes
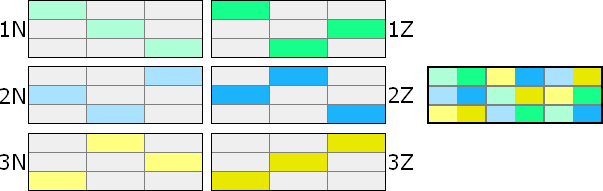
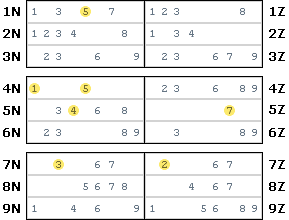
Here is a diagram that shows how the 3 digits that start in the top-left intersection can be distributed in the remainder of the chute. Each rectangle represents an intersection of a line and a box, which contains 3 cells.
As you can see, there are only 4 possible distribution patterns. In 3 of these patterns, there are 2 digits that travel together, while the 3rd digit travels in the opposite direction. This is what we call a braid. One of the patterns shows that all 3 digits travel in the same direction. We call this a rope. Braids are much more frequent than ropes, but if you like to see some, take a look at the canonical grid.
It is impossible for braids and ropes to mix in a single chute. So, when we discover a singe rope in a chute, all 9 digits must follow a rope pattern.
Strands
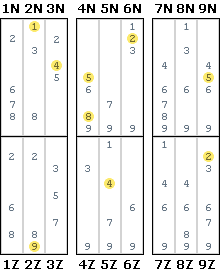
The next diagram shows the 6 ways to place a single digit in a chute. In Braiding Analysis we call these the strands. There is always a diagonal distribution pattern, which may wrap around.
The identifiers are formed by the starting position and the traveling direction. N represents a downward direction and Z the upward direction. On the right, a merged diagram shows to which 2 strands each intersection belongs.
Repeating Rules
As we have seen, digits only have limited ways to be organized in a chute. From these limitations, we can deduce a number of rules concerning repeating pairs.
- A pair of digits in one of the intersections in a chute can only appear in 0 or 2 other intersections in that chute.
- This rule is the direct result of the way digits are distributed in a chute. A pair will either repeat in all boxes of a chute or not at all.
- A pair of digits present in a boxrow can only appear in 0 or 1 boxcol in the tower that contains it.
- A pair of digits present in a boxcol can only appear in 0 or 1 boxrow in the floor that contains it.
- These rules are based on the fact that within a single box, a certain pair can only exist in a boxrow or a boxcol, but not in both. The crossing chute will have at least one intersection without that pair. Because there cannot be 2 pairs of the same digits in a chute, there can only be one or none at all.
- A pair of digits which repeats in a floor can only appear in 0 or 1 boxcol in each tower.
- A pair of digits which repeats in a tower can only appear in 0 or 1 boxrow in each floor.
- A direct extension of the previous rules.
Candidate Mapping
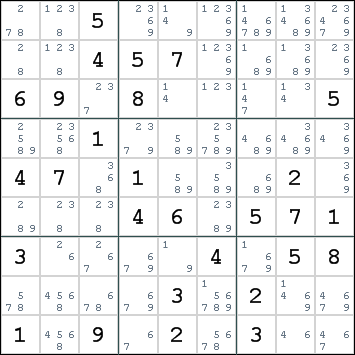
To enable us to analyze the strands, we must first map the candidates to those strands. This is a process that takes 2 steps. Here is a candidate grid that we will use as an example:
Step 1 - Candidates per intersection
In the first step, we collect all candidates which are present in each intersection. You need to do this twice. Once for the boxrows and once for the boxcols.
You do not need to highlight the placed digits, but it will be useful for the next step.
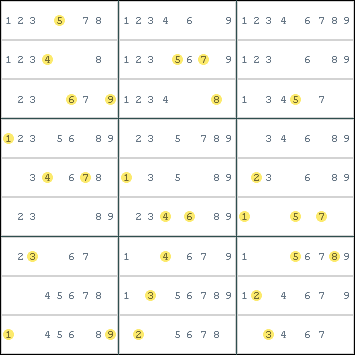
Step 2 - Digits per strand
In the second step, we collect all candidates which appear in all 3 intersections that belong to each strand. The result is a list of digits that each strand can contain.
The highlights show which digits are mandatory in their strands. You can set these when at least 2 intersections in the strand already contain this digit (using the highlights in the previous step) or when none of the 5 other strands in that floor allow this digit.
Pattern Analysis
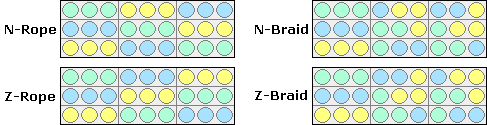
Each chute can be organized in one of 4 possible patterns.
These 4 patterns define how many digits will be assigned to N and Z strands:
- N-Rope
NNN
- N-Braid
NNZ
- Z-Braid
NZZ
- Z-Rope
ZZZ
There are a few rules that can help us eliminate some of these patterns:
- A fixed digit in any N strand eliminates the Z-Rope.
- A fixed digit in any Z strand eliminates the N-Rope.
- 2 fixed digits in any N strand eliminates the Z-Braid.
- 2 fixed digits in any Z strand eliminates the N-Braid.
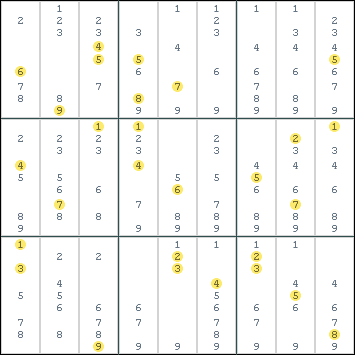
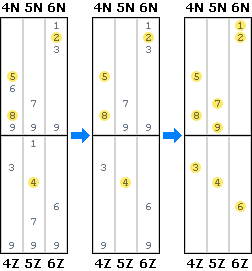
Analyzing Tower 2
Now we use these rules to reduce the number of possibilities in tower 2:
- Fixed digit 4 fixed in 5Z eliminates N-Rope.
- Fixed digits 58 in 4N eliminate Z-Rope and Z-Braid.
- The remaining pattern is N-Braid. Each N strand must contain 2 digits, each Z strand must contain 1 digit.
- Digits 69 eliminated from 4N, because it is saturated with 58.
- Digits 179 eliminated from 5Z, because it is saturated with 4.
- Digits 12 fixed in 6N, it is the only place they can go.
- Digits 79 fixed in 5N, because it must contain 2 digits and these are the only 2 left.
- Remaining digits 3 and 6 can now be fixed in strands 4Z and 6Z.
Drawbacks
Although the results that you can achieve with Braid Analysis look impressive, the same result can often be achieved with less complicated techniques. You should reserve it for Sudokus which cannot be advanced any further by the solving techniques that you are familiar with.
- Lateral thinking
- Braid Analysis forces you to look at a Sudoku from an unusual viewpoint. It takes a lot of practice to get used to it and draw the right conclusions.
- Laborious
- A lot of work is involved in candidate mapping. After each placement and elimination, you need to review and update the mapping.
- Error prone
- This is a serious issue. Without the help of a computer program, it is easy to make mistakes in candidate mapping which can lead to incorrect conclusions, preventing you from solving the puzzle.
Incidence
- The probability that there will be a rope [a repeating minirow] in at least one of the 6 bands is 24%
- The probability that any one band is of the "rope" pattern is 4 % [Approximately]
| This article is incomplete. You can help Sudopedia by expanding it. |