Pattern Overlay Method
The Pattern Overlay Method or POM analyzes the way digits can be placed in the remaining candidate space. This solving technique should be avoided when there are still a large number of available candidates in the grid.
Another name for this technique is templating.
Within the POM context, a pattern or template is a possible configuration for all instances a single digit that does not violate the Sudoku rule. For a standard Sudoku, there are 9 instances in each pattern. Here is an example:
There are 46656 different patterns. A single placement reduces this number by a factor 9. When a large part of the puzzle is solved, only a handful of patterns remain. At that point, the POM technique could be used by human solvers without too much effort.
How it works
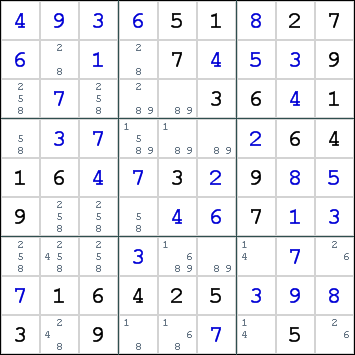
The first step is to isolate the remaining candidates for a single digit. In the following grid, we will analyze the possible patterns for digit 8.
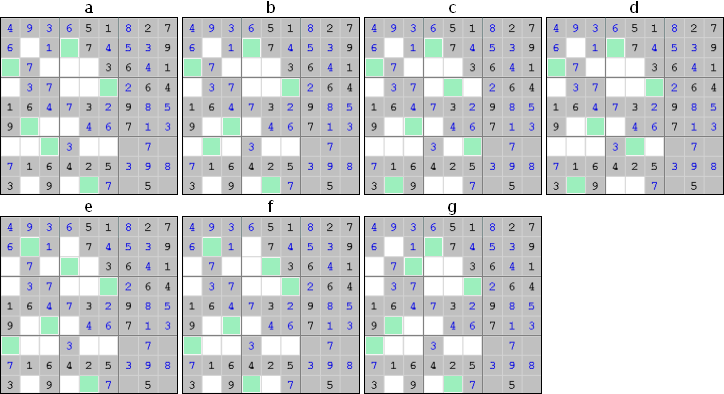
There are 7 patterns that can place the 6 remaining instances of digit 8 in the unsolved cells which allow this digit. They are identified by the letters a through g.
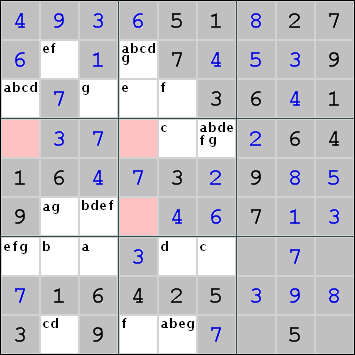
You do not need a separate grid for each pattern. It is also possible to write the pattern identifiers in a single grid. This grid then immediately shows the patterns used by each cell.
There are 2 possible deductions that you can make for a single-digit POM analysis:
- Cells which contain all pattern identifiers must contain the selected digit.
- Cells which contain no pattern identifiers cannot contain the selected digit.
In this example, there are 3 cells without any pattern identifiers. You can remove digit 8 from these cells.
Multiple Digits
When the POM method is ineffective for single digits, you can expand it by adding a second digit. Start with a cell that has 2 remaining candidates, a bivalue cell. Then use the POM analysis for both digits, analyzing the effects when either of the 2 digits is placed in that cell. In each case, the patterns of both digits cannot overlap. When the analysis is complete, you can make the same type of deductions as with the single digit method, which may also affect the starting cell.